To find the values of 𝑥 that make the expression 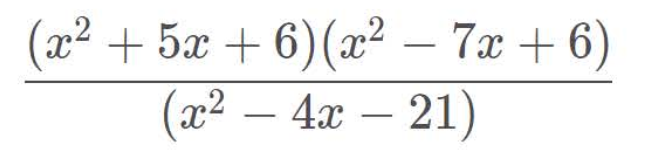 {(𝑥2+5𝑥+6)(𝑥2−7𝑥+6)}/(𝑥2−4𝑥−21) equal to zero, we need to find the values of 𝑥 that make the numerator equal to zero because division by zero is undefined.
{(𝑥2+5𝑥+6)(𝑥2−7𝑥+6)}/(𝑥2−4𝑥−21) equal to zero, we need to find the values of 𝑥 that make the numerator equal to zero because division by zero is undefined.
First, let’s factor the numerator and denominator:
Numerator: (𝑥2+5𝑥+6)(𝑥2−7𝑥+6)
(𝑥2+5𝑥+6) factors as (𝑥+2)(𝑥+3).
(𝑥2−7𝑥+6) factors as (𝑥−1)(𝑥−6).
So, the numerator becomes (𝑥+2)(𝑥+3)(𝑥−1)(𝑥−6).
Denominator: 𝑥2−4𝑥−21
This quadratic expression factors as (𝑥−7)(𝑥+3).
So, the expression becomes:
{(𝑥+2)(𝑥+3)(𝑥−1)(𝑥−6)}/{(𝑥−7)(𝑥+3)}
To make the expression equal to zero, the numerator must be zero, while the denominator should not be zero. So, the values of 𝑥 that make the expression equal to zero are the values that make the numerator zero:
𝑥=−2,𝑥=−3,𝑥=1,𝑥=6
However, we need to exclude any values that would make the denominator zero, which are 𝑥=−3 and 𝑥=7. Therefore, the possible values of 𝑥 are:
𝑥=−2,𝑥=1,𝑥=6

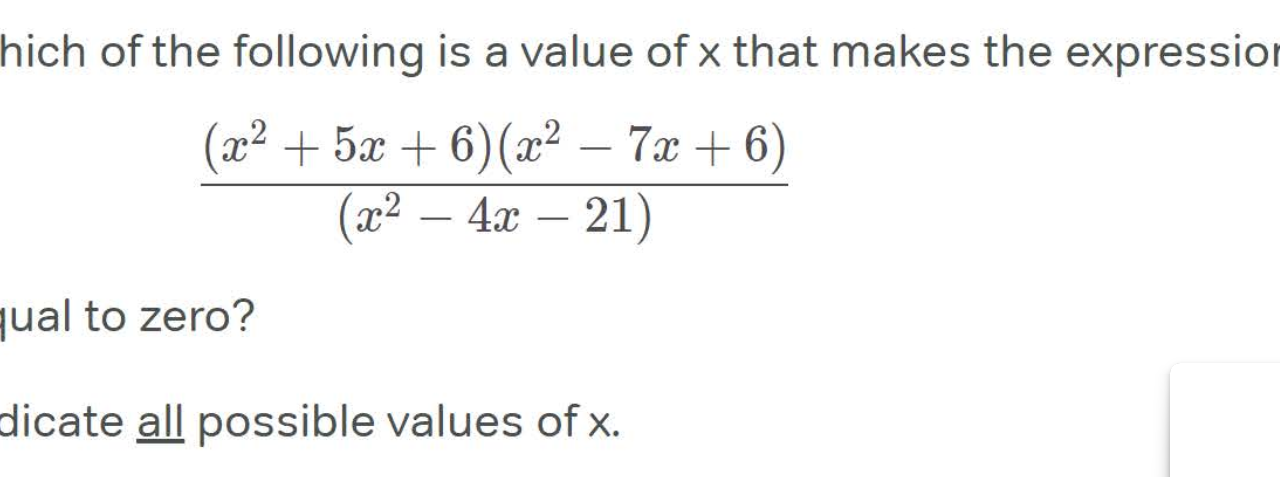



Recent Comments